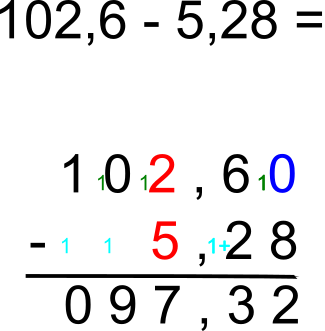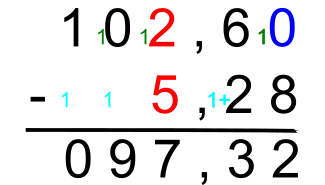1. Comment soustraire des entiers sans retenue ?
2. Comment soustraire des nombres à 2 chiffres avec retenue en utilisant la méthode par cassage 1/2 ?
3. Comment soustraire des grands nombres avec retenue en utilisant la méthode par cassage 2/2 ?
4. Comment soustraire des nombres à 2 chiffres avec retenue en utilisant la méthode classique 1/2 ?
5. Comment soustraire des grands nombres avec retenue en utilisant la méthode classique 2/2 ?
💡 Exemple
Il est impossible de calculer : 245 − 612 = car 245 < 612
Pour calculer : 1 096 − 568 =
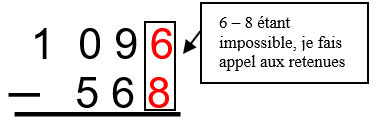👉 Bien vérifier que le nombre le plus grand est placé en haut et bien aligner le chiffre des unités.
On utilise la retenue quand le chiffre du haut est inférieur au chiffre au-dessous dans la même colonne.
👉 Il existe deux sortes de retenues :
- En haut, la retenue est à gauche du chiffre, elle se lit
- En bas, la retenue est à droite du chiffre et précédé d'un +, elle s’ajoute à ce chiffre.
- Les retenues vont toujours par paires : une en haut et une en bas.
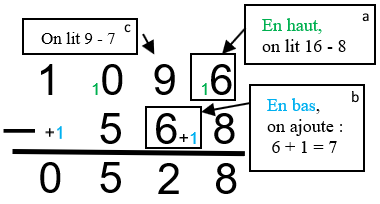
- 6 − 8 🖝 « C'est impossible. J'ajoute donc mes 2 retenues + 1 et 1 »
- Maintenant je peux dire : 16 − 8 🖝 « égale 8. »
- Ensuite, 9 − 7 (6 + ma retenue), c'est possible 🖝 « cela fait 2. »
- 0 − 5 🖝 « C'est impossible. J'ajoute donc mes 2 retenues + 1 et 1 »
- Maintenant je peux dire : 10 − 5 🖝 « égale 5. »
- Enfin, 1 − 1 🖝 « égale 0. »
- « Le résultat est donc 528. »
1 096 − 568 = 528
Il est impossible de calculer : 245 − 612 = car 245 < 612
Pour calculer : 1 096 − 568 =
👉 Bien vérifier que le nombre le plus grand est placé en haut et bien aligner le chiffre des unités.
On utilise la retenue quand le chiffre du haut est inférieur au chiffre au-dessous dans la même colonne.
👉 Il existe deux sortes de retenues :
- En haut, la retenue est à gauche du chiffre, elle se lit
- En bas, la retenue est à droite du chiffre et précédé d'un +, elle s’ajoute à ce chiffre.
- Les retenues vont toujours par paires : une en haut et une en bas.
- 6 − 8 🖝 « C'est impossible. J'ajoute donc mes 2 retenues + 1 et 1 »
- Maintenant je peux dire : 16 − 8 🖝 « égale 8. »
- Ensuite, 9 − 7 (6 + ma retenue), c'est possible 🖝 « cela fait 2. »
- 0 − 5 🖝 « C'est impossible. J'ajoute donc mes 2 retenues + 1 et 1 »
- Maintenant je peux dire : 10 − 5 🖝 « égale 5. »
- Enfin, 1 − 1 🖝 « égale 0. »
- « Le résultat est donc 528. »
1 096 − 568 = 528
💡 Autre exemple
Pour calculer : 1 197 − 568 =
1 197 − 568 = 629
Pour calculer : 1 197 − 568 =
1 197 − 568 = 629
ℹ️ Retenir
🖝 La soustraction permet de calculer un écart, une différence.
🖝 Avant de calculer, j'évalue l'ordre de grandeur du résultat.
Pour calculer : 1 197 − 568 👉 j'arrondis les nombres : 1 200 − 600 ≈ 600
🖝 Quand je pose la soustraction, je n'oublie pas d'aligner les chiffres de même classe en m'aidant de la réglure de mon cahier.
Je n'oublie pas les retenues qui vont toujours par paires.
Rappel : 👉 Il existe deux sortes de retenues :
- En haut, la retenue est à gauche du chiffre, elle se lit
- En bas, la retenue est à droite du chiffre, elle s’ajoute à ce chiffre.
- Les retenues vont toujours par paires : une en haut et une en bas.
On peut vérifier son calcul en effectuant l'addition inverse :
568 + 629 = 1 197
🖝 La soustraction permet de calculer un écart, une différence.
🖝 Avant de calculer, j'évalue l'ordre de grandeur du résultat.
Pour calculer : 1 197 − 568 👉 j'arrondis les nombres : 1 200 − 600 ≈ 600
🖝 Quand je pose la soustraction, je n'oublie pas d'aligner les chiffres de même classe en m'aidant de la réglure de mon cahier.
Je n'oublie pas les retenues qui vont toujours par paires.
Rappel : 👉 Il existe deux sortes de retenues :
- En haut, la retenue est à gauche du chiffre, elle se lit
- En bas, la retenue est à droite du chiffre, elle s’ajoute à ce chiffre.
- Les retenues vont toujours par paires : une en haut et une en bas.
On peut vérifier son calcul en effectuant l'addition inverse :
568 + 629 = 1 197
Télécharger le fichier
pdf
