1. Quelle opération permet de partager ?
💡 Retenir
Quelle est la meilleure technique pour partager ?
Il existe plusieurs techniques pour partager.



👉 Utiliser les tables de multiplications nous facilite le travail. C'est la plus efficace des techniques.
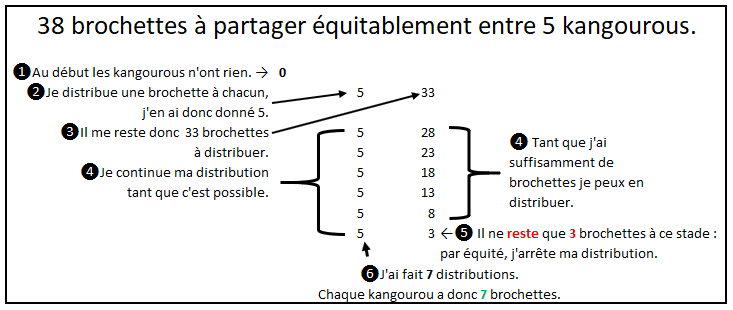
On cherche dans la table du 5 un résultat proche de 38 (mais qui reste inférieur à 38) : 7 × 5 = 35
38 = (7 × 5) + 3.
2. Comment répartir un trésor entre plusieurs personnes ?
💡 Retenir
Récapitulons
Un peu de vocabulaire de technicien...

👉 Rechercher dans les tables de multiplications le multiple le plus proche.
On cherche dans la table du 4 un résultat proche de 34 (mais qui reste inférieur à 34) : 8 × 4 = 32
34 = (8 × 4) + 2.
On peut aussi écrire le résultat sous cette forme : 34 ÷ 4 = 8 et il reste 2.
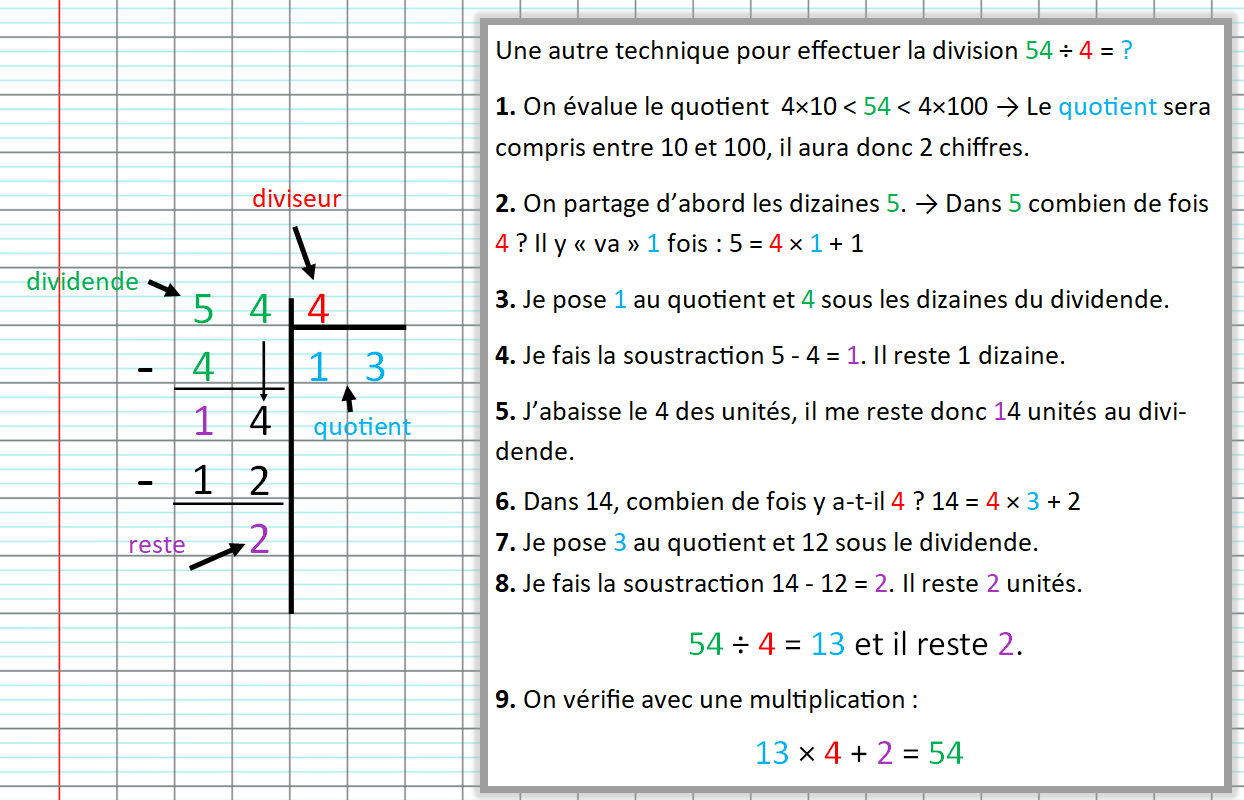
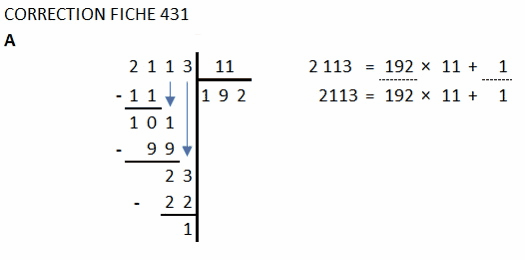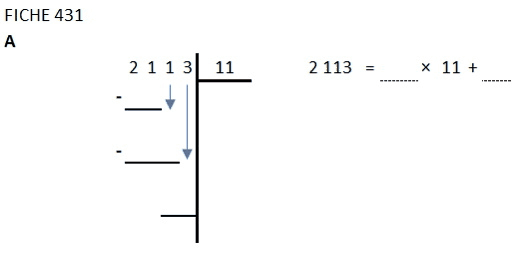
3. Comment utiliser les multiples pour diviser ?
💡 Rappel
Comment reconnaitre les multiples de 2, 3, 5, 9, 10 ?
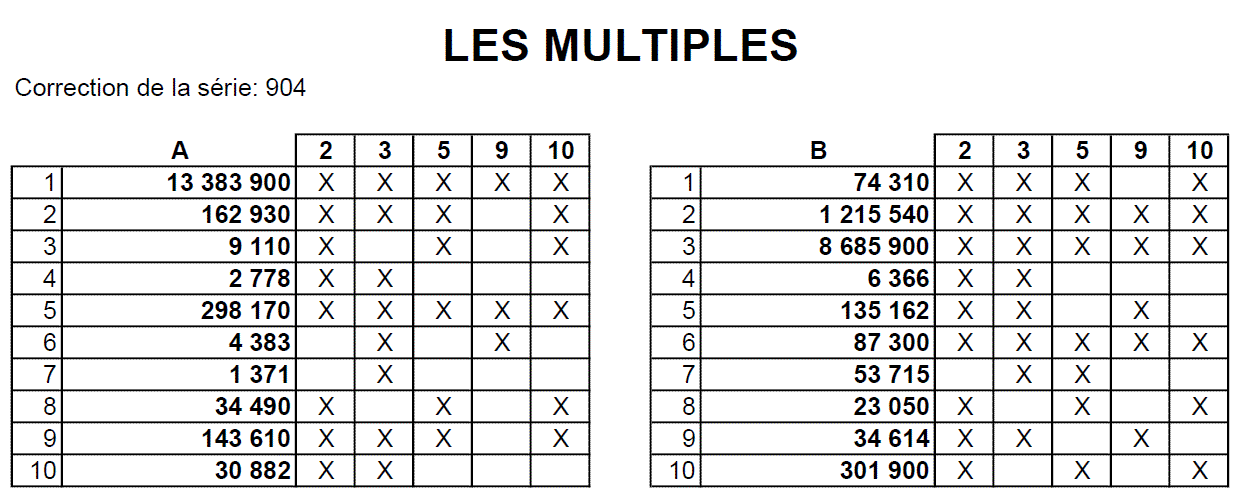
Quelques règles…
👉 Les multiples de 2 sont des nombres pairs. Ils se terminent par « 0, 2, 4, 6 ou 8 ».
Exemples : 12, 116, 8, 110 sont des multiples de 2.
👉 Les multiples de 3 sont des nombres dont la somme des chiffres est un multiple de 3.
Exemples de multiples de 3 :
135 (car 1 + 3 + 5 = 9), et 9 est dans la table de 3.
6 213 (car 6 + 2 + 1 + 3 = 12), et 12 est dans la table de 3.
👉 Les multiples de 5 sont des nombres qui se terminent par 0 ou 5.
Exemples de multiples de 5 :
135, 2 015, 3 000…
👉 Les multiples de 9 sont des nombres dont la somme des chiffres est égale à 9.
Exemples de multiples de 9 :
135 (car 1 + 3 + 5 = 9), et 9 est dans la table de 9.
516 213 (car 5 + 1 + 6 + 2 + 1 + 3 = 18), et 18 est dans la table de 9.
👉 Les multiples de 10 sont des nombres qui se terminent par 0.
Exemples de multiples de 10 : 530, 9 210, 540…
👉 Certains nombres peuvent être multiples en même temps de 2, 3, 5, 9, 10 .
Exemples de multiples de 2, 3, 5, 9, 10 : 52 110, 450, 180, 64 710…
4.Comment trouver le nombre de parts égales en divisant ?
💡 Retenir
👉 Pour partager, on utilise une division. Le résultat s’appelle le quotient.
A l'aide des tables de multiplications on cherche le multiple le plus proche.
On cherche dans la table du 4 un résultat proche de 24 : 6 × 4 = 24
On peut aussi écrire : 24 ÷ 4 = 6 ou 24 ÷ 6 = 4
24 ÷ 6 = 4 → 4 est le quotient et 6 est le diviseur 24 est le dividende. Il n'y a pas de reste.
58 ÷ 7 = 8 et il reste 2. → 8 est le quotient et 7 est le diviseur 58 est le dividende. Le reste est 2.
Le reste est inférieur au diviseur, la division est terminée.
5. Comment calculer la valeur d'une part ?
6. Comment comprendre le reste de la division ?
💡 Retenir
Une division « ne tombe pas toujours juste »... Il peut y avoir un reste.
64 ÷ 5 = 12 reste 4
818 ÷ 100 = 8 reste 18